[컴퓨터 구조] 챕터5 리뷰

Memory Hierarchy

• Processcor - Memory - Memory ... 
• higher the level(closer to the CPU) = smaller, more expensive($), faster
• Principle of locality
  • temporal locality: recent items are likely to be accessed again soon
  • spatial locality: items near recent items are likely to be access soon
  • data is copied between only two adjacent levels at a time
  • lowest level(HDD) must have all data (= store everything on disk)
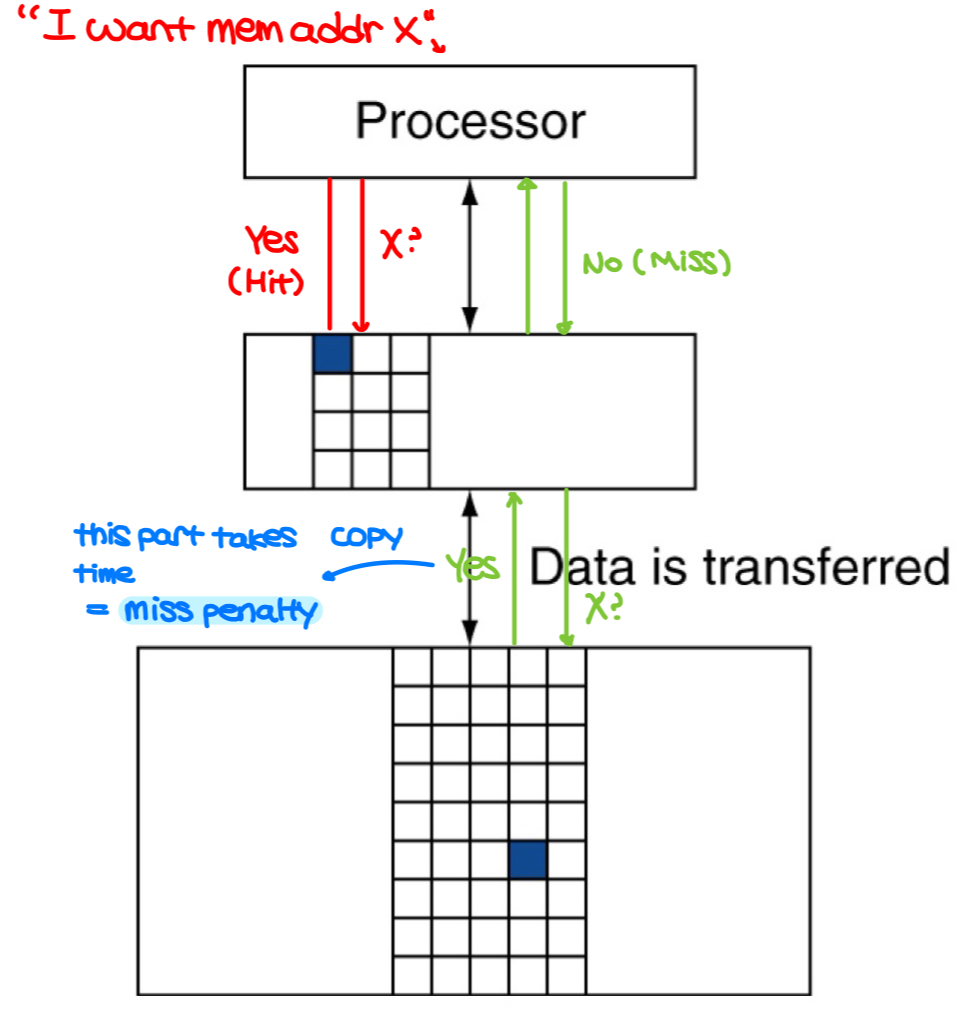
• Memory hierarchy levels
  • block(line): unit of copying (may be multiple words)
  • hit: data is in upper level
  • miss: data is absent and is copied from lower level
    • time taken = miss penalty
    • miss ratio = misses/accesses = 1 - hit ratio

 

• SRAM
  • data stored using 6-8 transistors for one bit
  • expensive, fast (fixed access time to any datum)
• DRAM
  • single transistor for one bit
  • needs to be periodically refreshed
  • follows Moore's Law
• Flash storage
  • non-volatile semiconductor storage (a type of EEPROM)
  • wears out after 1000's of accesses
  • not suitable for direct RAM or disk replacement
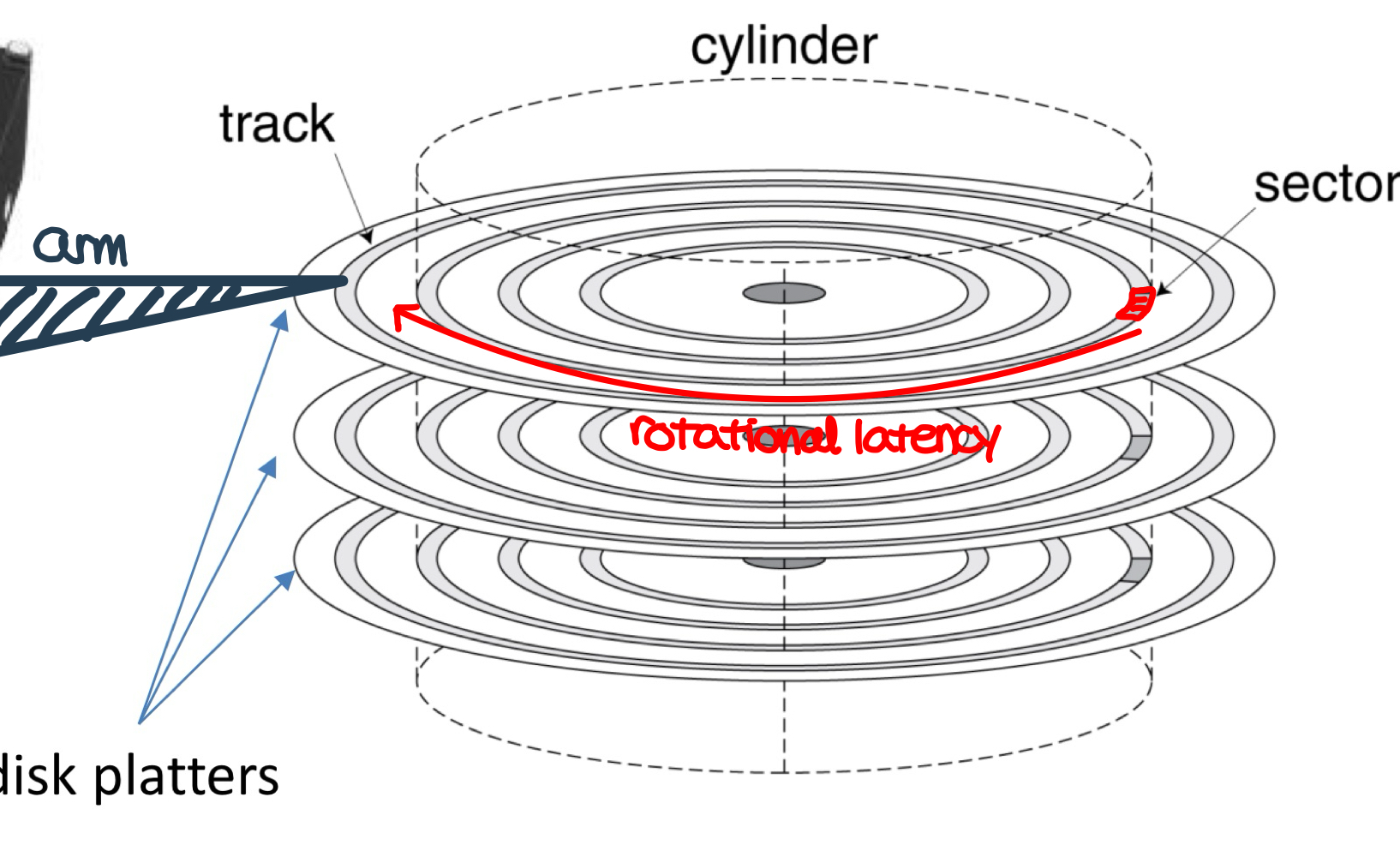
• Disk storage
  • non-volatile, rotating magnetic storage
  • the arm finds the right track
  • each sector records sector ID, data, error correcting code, synchronization fields and gaps
  • access to a sector involves queuing delay if other access are pending, rotational latency, data transfer and controller overhead
   

 

• The basics of cache memory
  • it's the level of hierarchy closest to the CPU
  • if instruction is given, how do we know where to look/put?
    • direct-mapped, fully associative, M-way set associative
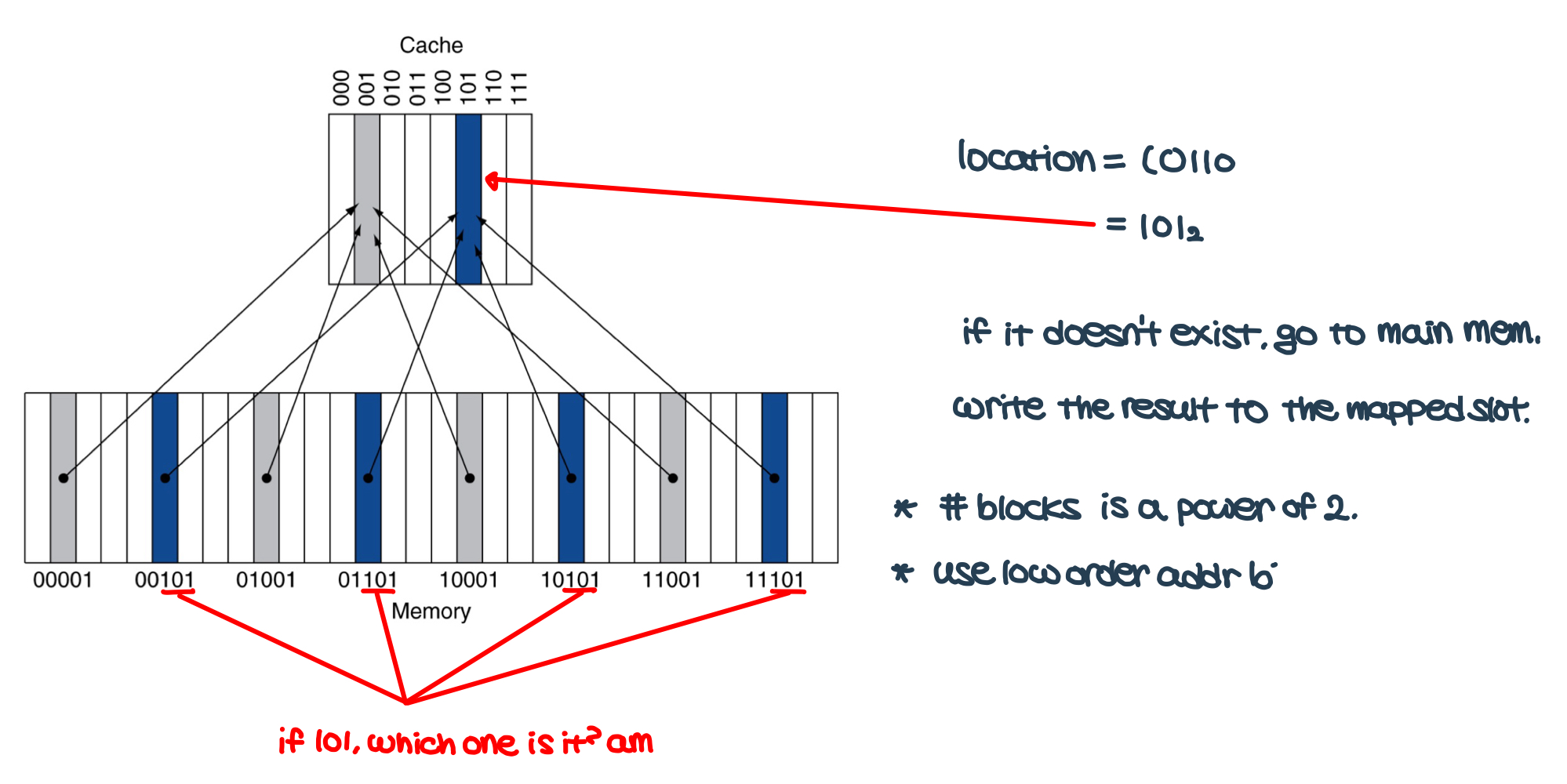
• Direct mapped cache
  • put/look location is determined by address
  • location = (block address) mod (# of blocks in cache)
  • however, ambiguity exists -> solved by using tags and valid bits
   

 

• Direct mapped cache (cont.)
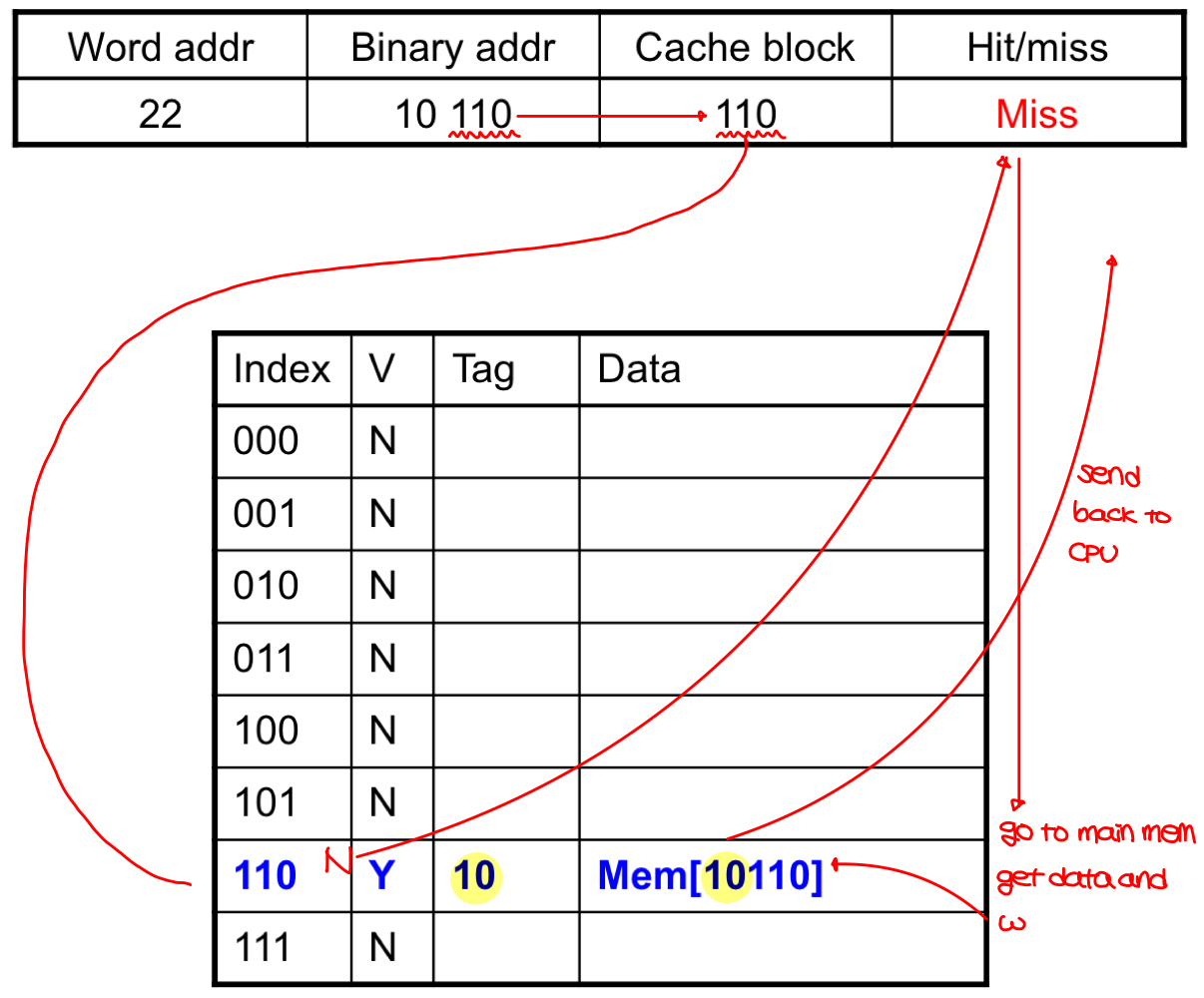
  • tags are used for knowing which block is stored in a cache location.
  • stores block address and the data.
  • only the high-order bits(tag) are used. The lower three bits are ignored.
  • valid bit is set to 1 if data is present, 0 if not.
  • if data exists, but the tags don't match, go to the main memory, copy data, come back to the cache, change the tag and the data, and write back to the CPU.
   

 

 

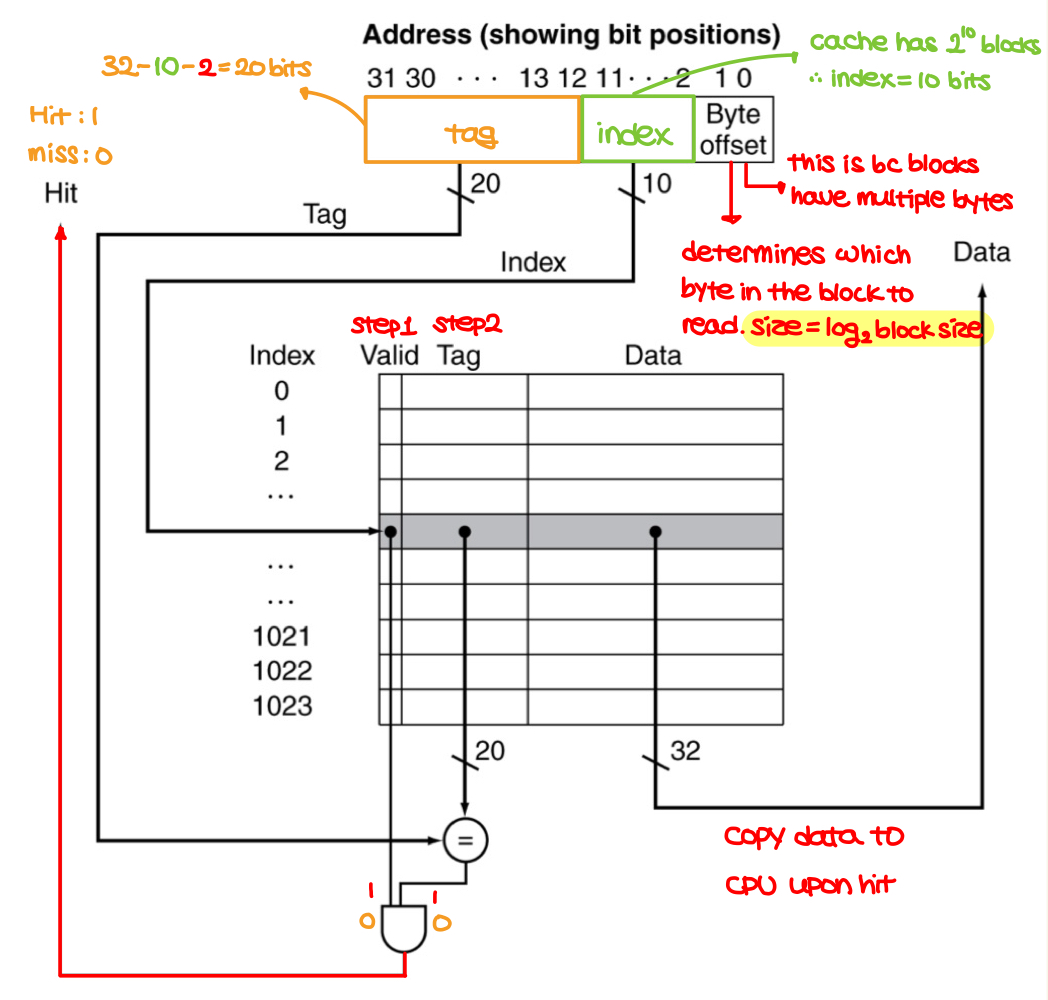
• Example of direct-mapped cache
  • the byte offset determines which byte in the instruction to read.
  • For example, if a block has 16(2^4) bytes, the byte offset would be 4 bits, as there are 4 words.

 

• Block size considerations
  • in fixed-sized cache, larger blocks -> more competition for memory space, which increases miss rate
  • there could also be pollution (unwanted data)
  • large block size also causes large miss penalty as lot of time is spent copying.
  • if block size is too small or too large, the miss rate increases. We have to find the Goldilocks zone
• Cache (read) misses
  • one cache hit, proceed normally without stalling
  • on miss
    • stall the pipeline
    • fetch the block from the next level of hierarchy
    • restart cache access
• Cache (write) misses
  • on hit, just update the block in cache
  • if 'store' writes to only the cache, then memory-cache inconsistency occurs
• Write-through
  • always update both the cache and the memory
  • simple, but inefficient
• Write-back
  • update only the cache and write the modified block to memory when it's replaced
  • usually faster, but more complex
• Write allocation
  • for write-through, there are two alternatives (no better/worse):
    • allocate on miss: fetch the block; write directly to the main memory, copy the written data to the cache
    • write around: don't fetch; write directly to the main memory, but don't copy
• Measuring cache performance
  • CPU time = CPU execution time + memory stall time (includes cache hit time)
  • data memory stall cycles = memory accesses * miss rate * miss penalty
  • instruction memory stall cycles = memory accesses * miss rate * miss penalty
• Average access time
  • hit time is also important
  • average memory access time(AMAT) = hit time + miss rate * miss penalty
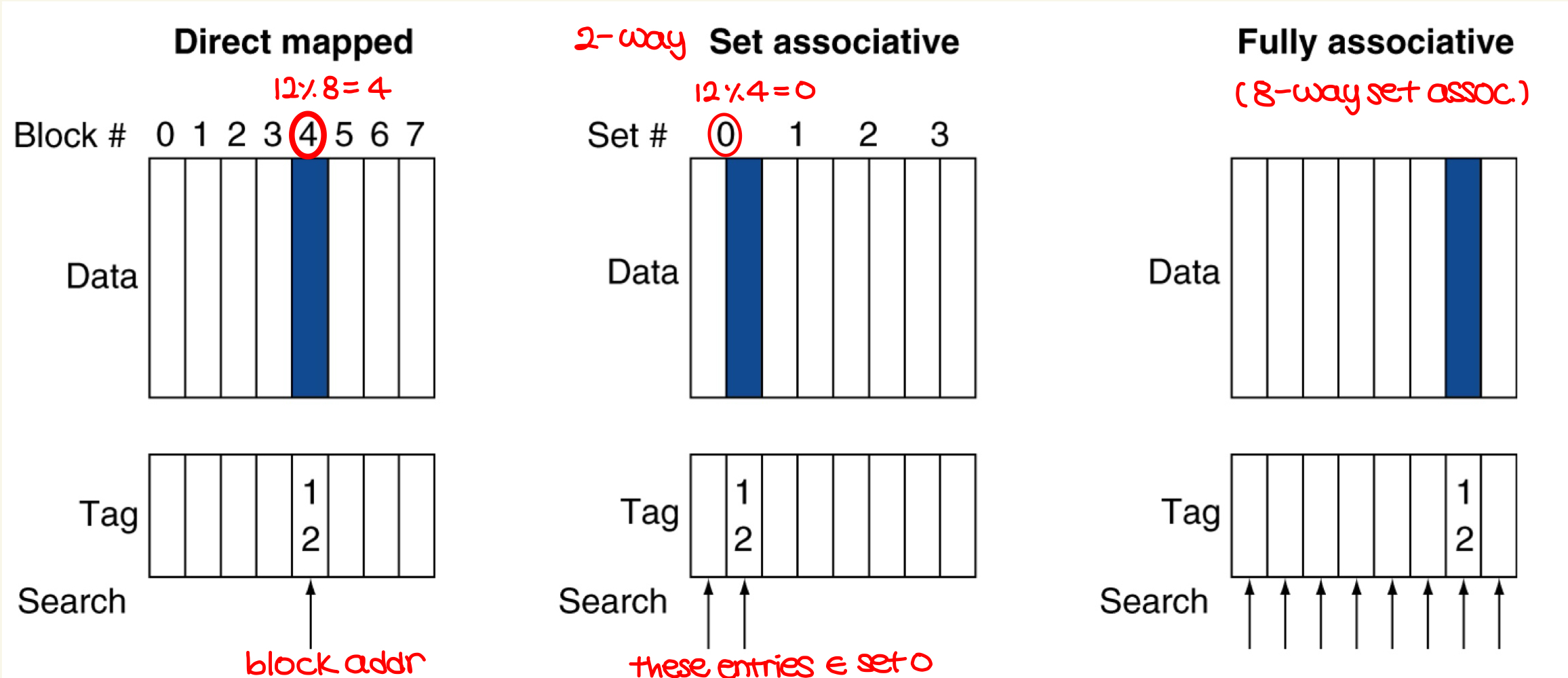
• Associative caches
  • fully associative
    • blocks can go to any cache entry
    • more flexible, low miss rate, but expensive
    • all entries are searched at once
  • M-way set associative
    • each set contains M entries
    • block number determines the set number. i.e., set = (block #) mod (# of sets)
    • all entries in a set is searched at once
     

 

• Increased associativity means decreased miss rate, but with diminishing returns + more cost, more search time
• Replacement policy
  • direct mapped caches -> no choice
  • associative caches -> if there's no valid entry, use LRU or random replacement method
• Multilevel cache
  • CPU - L1 cache - L2 cache - main memory
  • multiple caches
• SW optimization for lowering miss rate is also possible. Use principle of locality to reduce miss rate.
• Encoding/decoding
  • often used for error detection
  • if error is detected, drop data and try again or fix error
• Hamming code
  • Hamming distance: number of bits that are different between two bit patterns
  • if we increase the Hamming distance too much, then the range of legal bit patterns decrease
  • minimum distance of 2 provides single bit error detection (even/odd parity)
    • ex) 00011111 -> 000111111 (if # of 1s is odd, add 1 to the end. This guarantees even # of 1s)
  • minimum distance of 3 provides single and double bit error detection. (Hamming SEC/DEC)
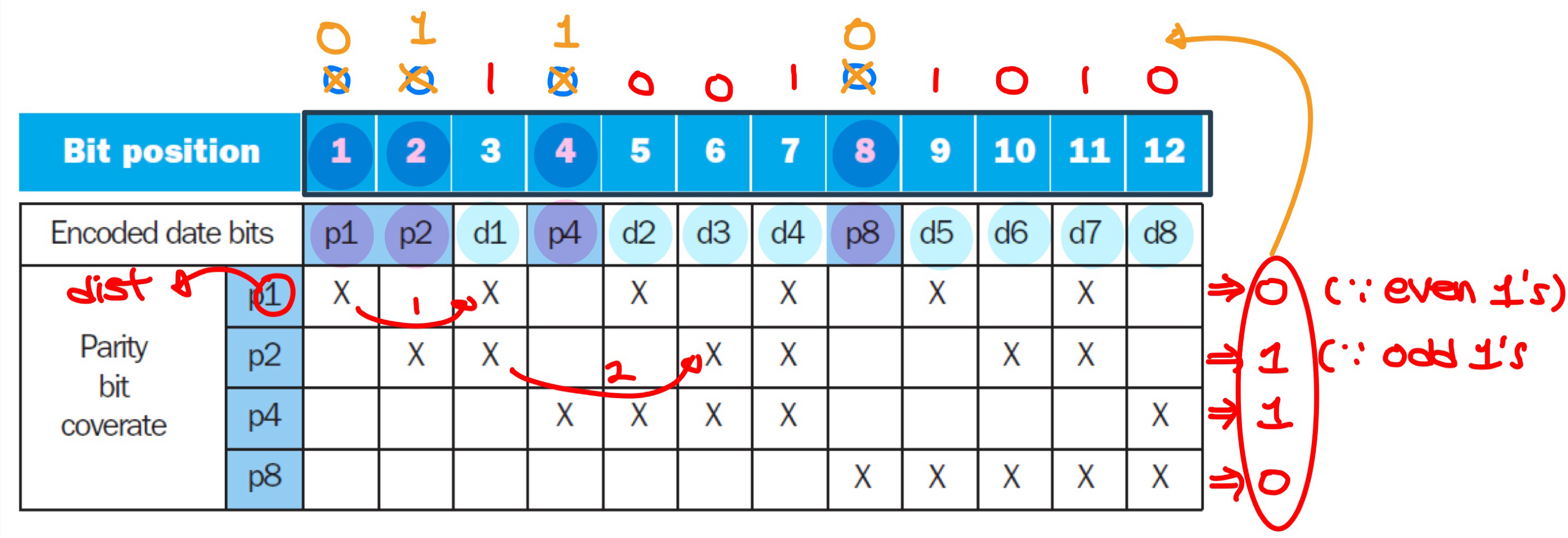
• Encoding Hamming SEC
  • number bits from 1 on the left, including data bits $d$ and parity bits $p$
  • all bit positions that are a power of 2 = parity bits
  • initialize parity bits to zero
  • each parity bit checks certain data bits (marked by X)
   

 

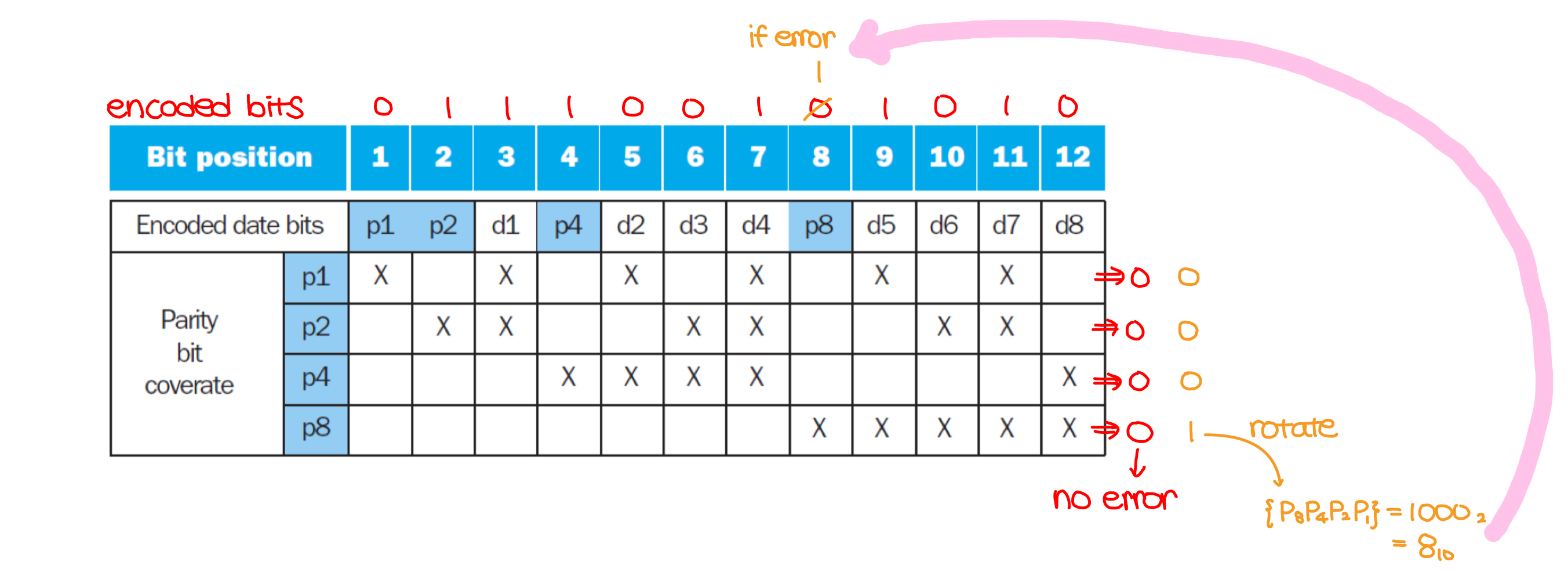
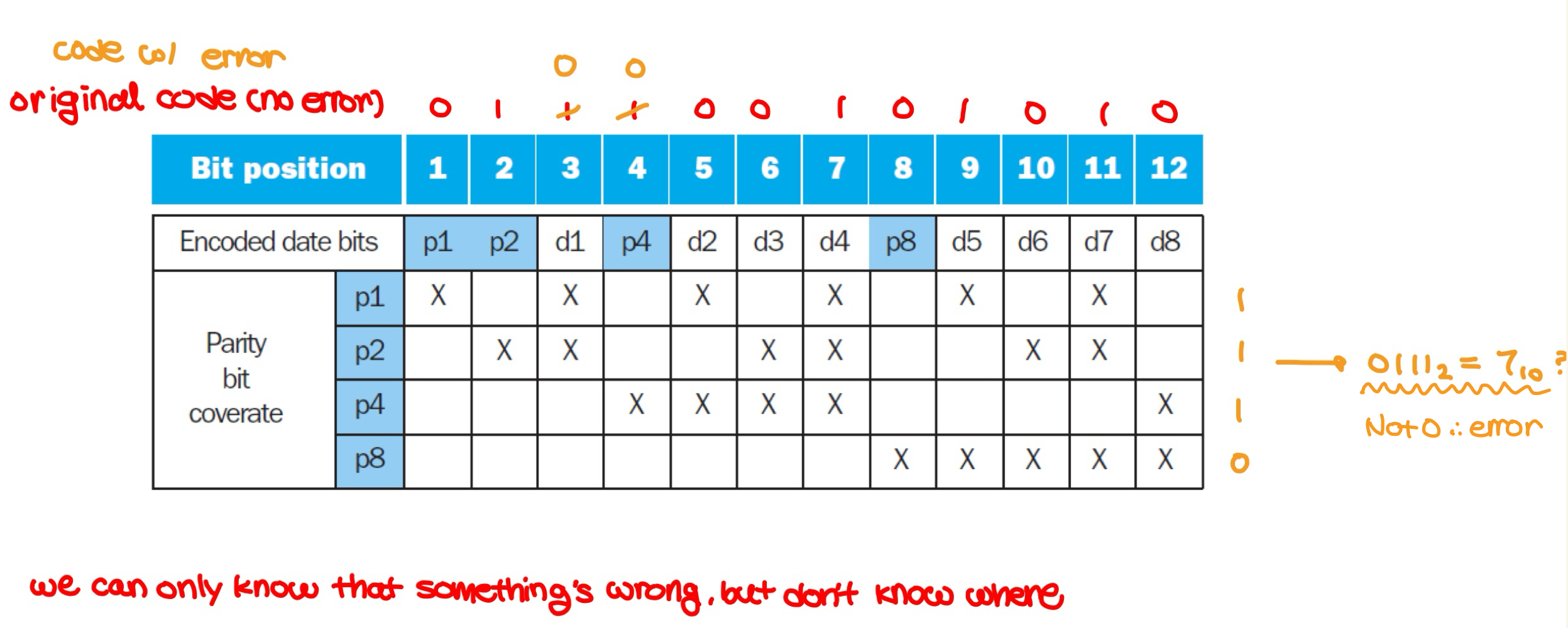
• Decoding Hamming SEC
  • re-calculate the parity bits from the encoded code
  • the values of parity bits indicate which bits are in error
   

 

• Two-bit errors in Hamming SEC

 

 

• SEC/DED code 
  • add an additional bit $P_{n}$ for the whole SEC code
  • make Hamming distance = 4

 

 

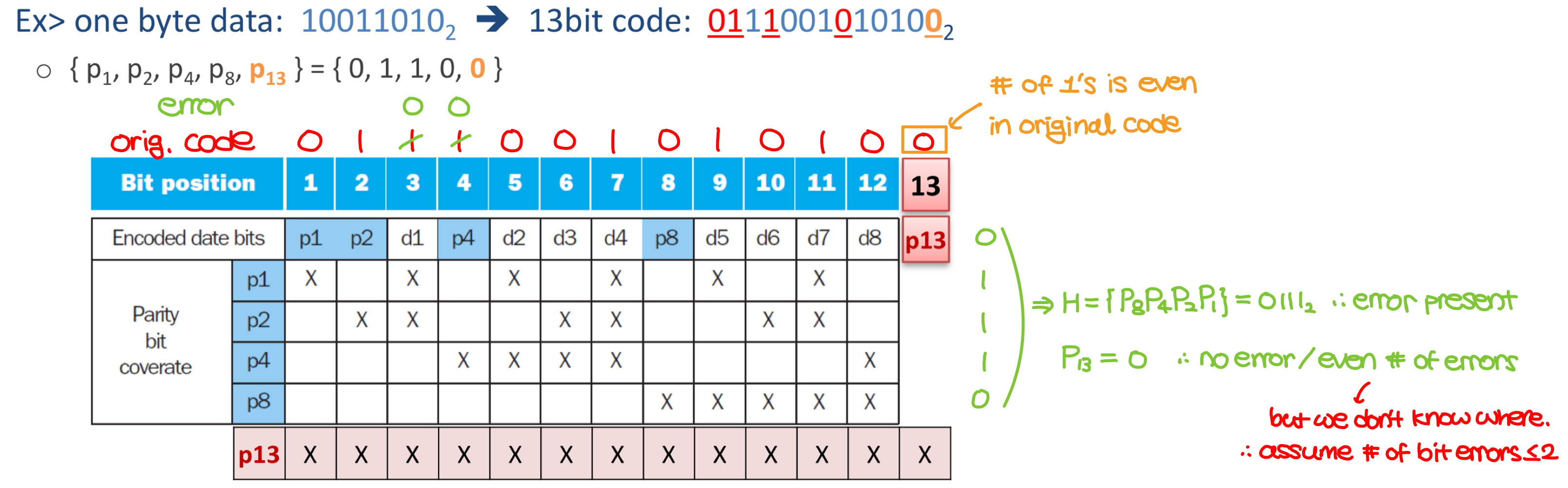
• Decoding scheme for the above example
  • {$H$ even, $P_{n}$ even} -> no error
  • {$H$ odd, $P_{n}$ odd} -> correctable single bit error
  • {$H$ even, $P_{n}$ odd} -> error in $P_{n}$
  • {$H$ odd, $P_{n}$ even} -> even number of errors
    • we assume this to be 2. If there are more than two errors, get a new networking system.

 

Virtual Memory

• Some problems
  • multiple programs want to use single main memory simultaneously
  • program A wants to use 2GB of memory, but my computer only has 1GB
• Virtual memory
  • allows programs to exceed the size of the primary memory
  • use main memory as a "cache" for secondary storage
  • programs share main memory
    • each program gets a private virtual address space (later translated to physical address) holding its frequently used data

 

 

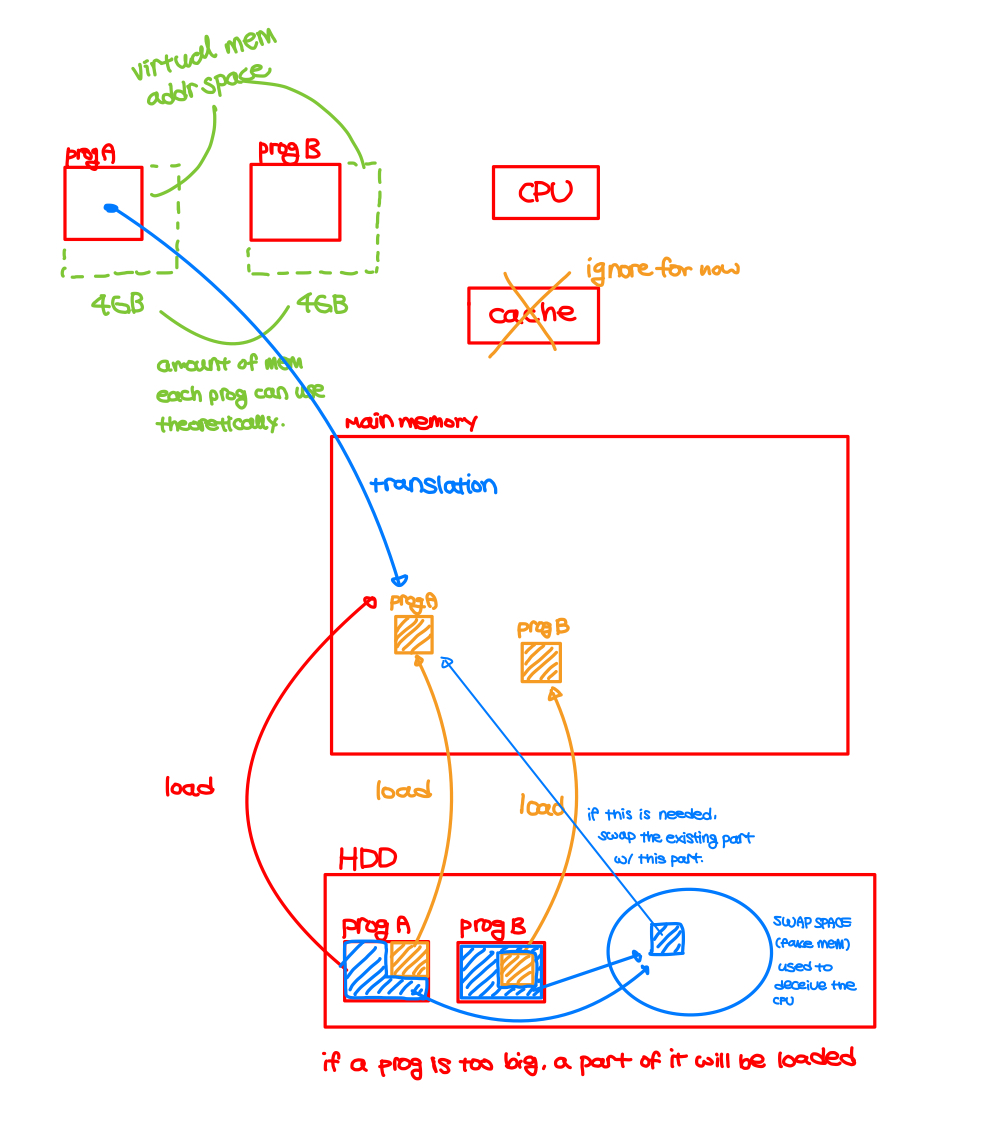
• Translatiion
  • virtual memory "block" = page
  • translation miss = page fault -> page needs to be fetched from the disk, takes millions of cycles
  • relocation: map virtual address -> physical addresses before using them to access memory.
    • this allows loading program anywhere in the memory as a set of pages 

 

 

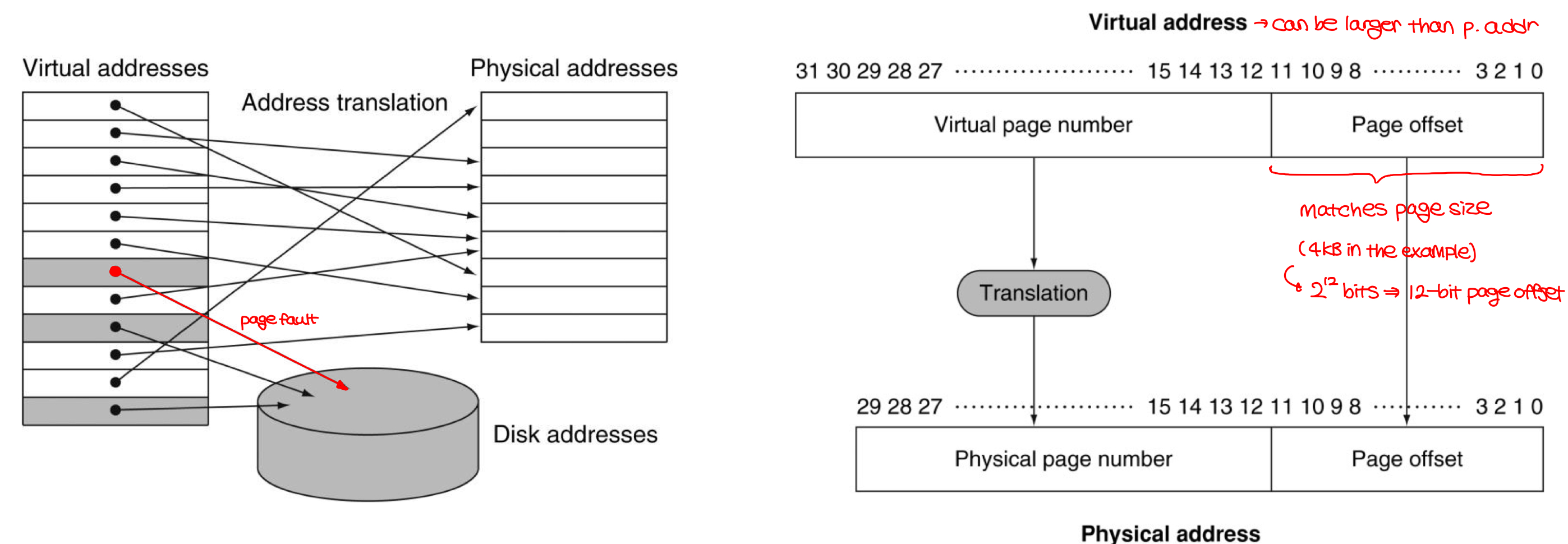
• Page table (uses LRU)
  
  • stores placement information
  • array of page table entries (PTE) indexed by virtual page number
  • page table register in the CPU points to the page table in the physical memory

 

 

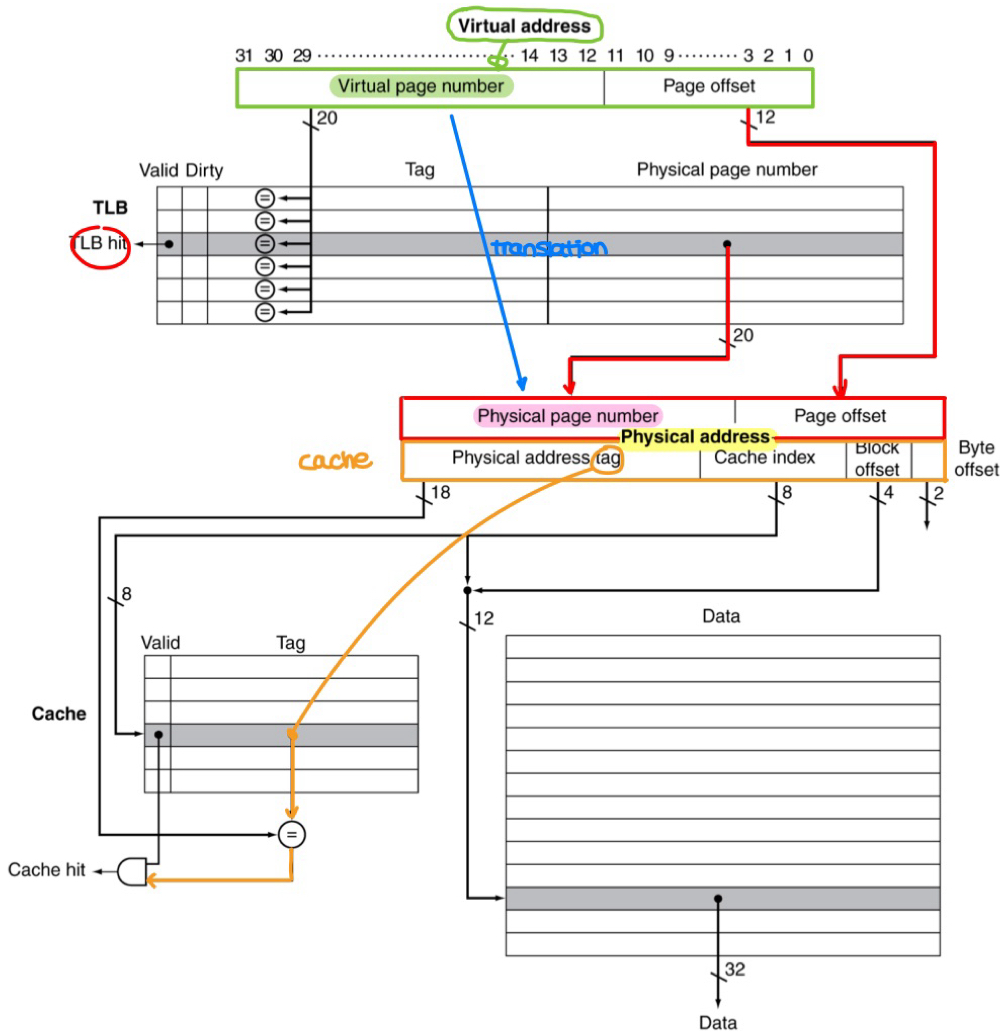
• Fast translation using TLB (translation look-aside buffer)
  • address translation would appear to require extra memory reference (PTE + actual memory)
  • however, access to page tables has a good locality (0.01% ~ 0.1% miss rate)

 

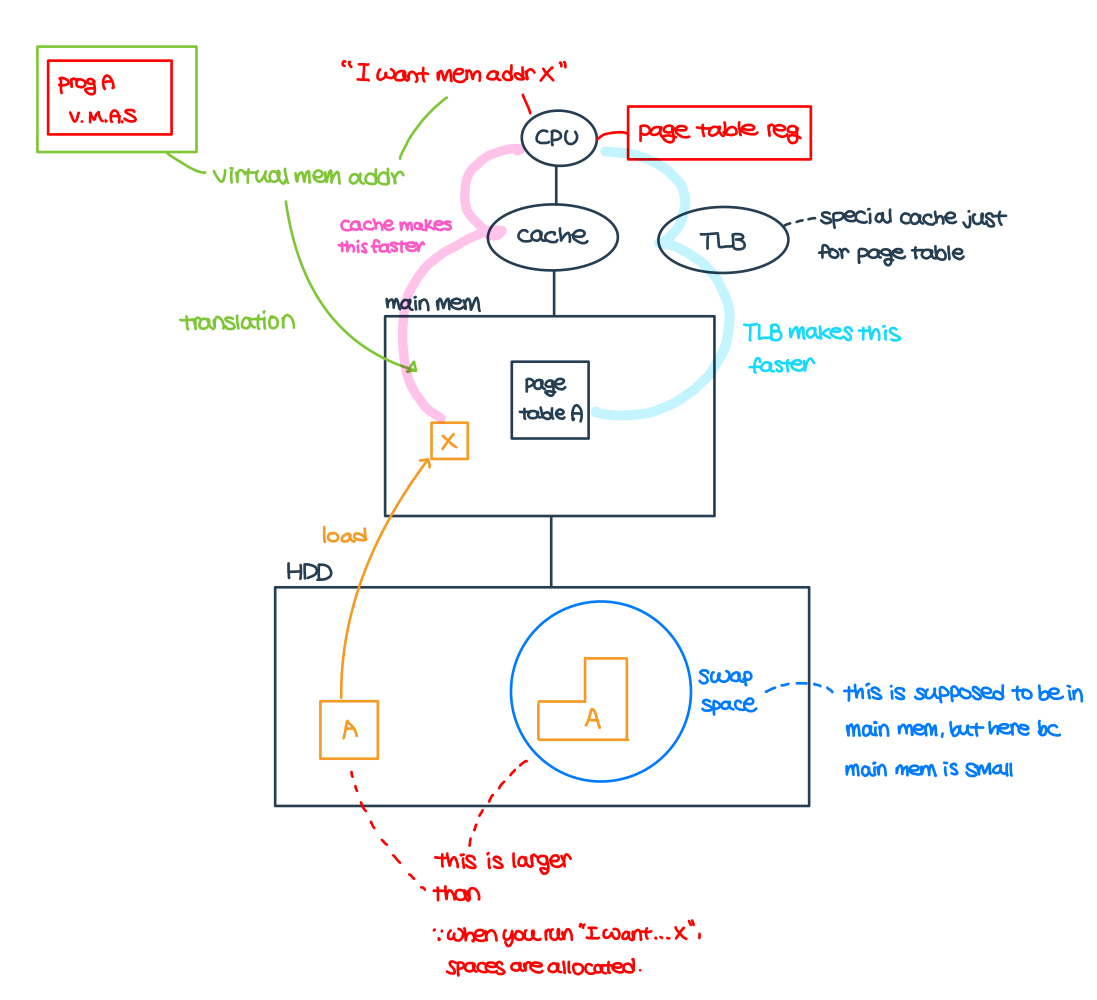
• TLB misses
  • page is present in memory but the PTE is not in TLB or, 
  • page is not present in memory (= page fault)
• Page fault handler (was on the final exam)
  • use the faulting virtual address to find the PTE
  • locate page on disk 
  • choose page to replace
  • read page into memory, update the page table
  • restart from the faulting instruction
• TLB-cache interaction

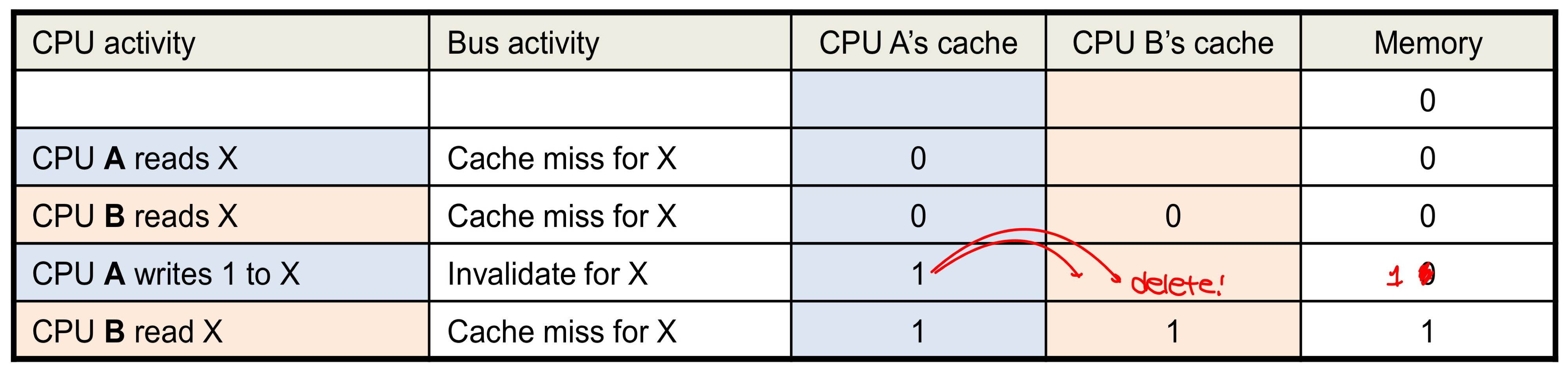
• Cache coherence problem

 

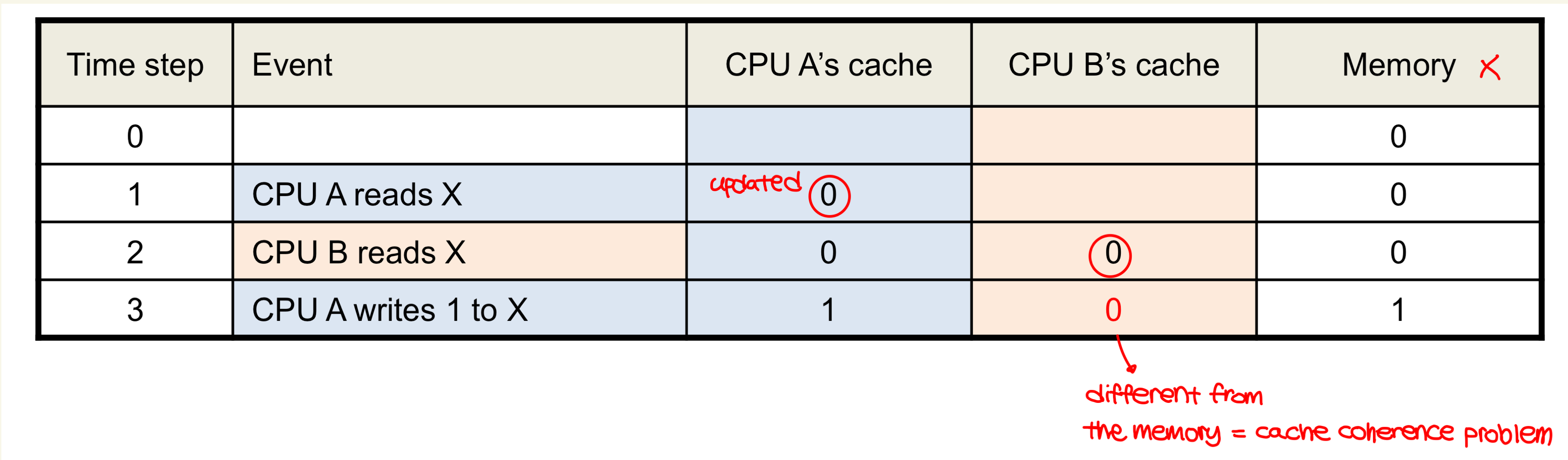
• Cache coherence problem is solved by cache coherence protocols which are performed by caches to ensure coherence.